Primer

This document covers the main areas of pyGPlates functionality, and some plate tectonic foundations.

Plate reconstruction hierarchy

Note

Next-generation plate-tectonic reconstructions using GPlates contains a good introduction to plate reconstruction hierarchies.

A plate-reconstruction hierarchy consists of a tree of total reconstruction poles at an instant in geological time.

Plate motions are described in terms of relative rotations between pairs of plates. Every plate in the model moves relative to some other plate where, within each of these plate pairs, one plate is considered the moving plate relative to the other fixed plate. That fixed plate, in turn, moves relative to another plate thus forming a tree-like structure known as the reconstruction tree. Each of these relative rotations is an edge in the tree.

The following diagram shows a subset of the hierarchy of relative rotations used in GPlates:

             000
              |
              |  finite rotation (001 rel. 000)
              |
             001
              |
              |  finite rotation (701 rel. 001)
              |
             701(AFR)
             /|\
            / | \  finite rotation (802 rel. 701)
           /  |  \
        201  702  802(ANT)
         /   / \    \
        /   /   \    \  finite rotation (801 rel. 802)
       /   /     \    \
    202  704     705  801(AUS)
    / \
   /   \
  /     \
290     291

…where 000 is the anchored plate (the top of the reconstruction tree). The edge 802 rel. 701 contains the rotation of 802 (the moving plate in the pair) relative to 701 (the fixed plate in the pair).

An equivalent rotation is the rotation of a plate relative to the anchored plate. So the equivalent rotation of plate 802 is the composition of relative rotations along the plate circuit edge path from anchored plate 000 to plate 802.

A relative rotation is the rotation of one plate relative to another plate (as opposed to the anchored plate). Note that, like equivalent rotations, the plate circuit edge path can consist of one or more edges. For example, the rotation of plate 801 relative to plate 291 follows an edge path that goes via plates 202, 201, 701 and 802. However it should be noted that if the edge between 001 and 701 did not exist then, even though a path would still exist between 291 and 801, the relative rotation (and equivalent rotations of 291 and 801 for that matter) would be an identity rotation. This is because the sub-tree below 001 would not get built into the reconstruction tree and hence all plates in the sub-tree would be missing. This can happen when the rotation sequence for a moving/fixed plate pair (eg, 701/101) does not span a large enough time period. You can work around this situation by setting the anchor plate to the relative plate (eg, 291 in the above example).

A total rotation is a rotation at a time in the past relative to present day (0Ma). In other words from present day to a past time.

A stage rotation is a rotation at a time in the past relative to another time in the past.

Working with finite rotations

A finite rotation represents the motion of a plate (relative to another plate) on the surface of the globe over a period of geological time.

In pyGPlates, finite rotations are represented by pygplates.FiniteRotation.

In the following sections we will first cover some rotation maths and then derive the four fundamental finite rotation categories:

In pyGPlates, these can be obtained from a pygplates.RotationModel.

Composing finite rotations

In the following examples a composed rotation \(R2 \times R1\) means the rotation \(R1\) is the first rotation to be applied followed by the rotation \(R2\) such that a geometry is rotated in the following way:

\[\begin{split}\text{geometry_final} &= R2 \times(R1 \times \text{geometry_initial}) \\ &= R2 \times R1 \times \text{geometry_initial}\end{split}\]

…which is the equivalent of…

\[\begin{split}\text{geometry_intermediate} &= R1 \times \text{geometry_initial} \\ \text{geometry_final} &= R2 \times \text{geometry_intermediate} \\ &= R2 \times (R1 \times \text{geometry_initial}) \\ &= R2 \times R1 \times \text{geometry_initial}\end{split}\]

Note

Rotations are not commutative (\(R2 \times R1 \neq R1 \times R2\))

The composed rotation \(R2 \times R1\) can be written in pyGPlates as either:

R2 * R1

…or…

pygplates.FiniteRotation.compose(R2, R1)

For example, the above geometry rotation can be written as either:

geometry_final = R2 * R1 * geometry_initial

…or…

geometry_final = pygplates.FiniteRotation.compose(R2, R1) * geometry_initial

Plate circuit paths

The rotation from present day (0Ma) to the geological time \(t_{2}\) (via time \(t_{1}\)) is given by:

\[R(0 \rightarrow t_{2}) = R(t_{1} \rightarrow t_{2}) \times R(0 \rightarrow t_{1})\]

…or by post-multiplying both sides by \(R(t_{1} \rightarrow 0)\), and then swapping sides, this becomes…

\[\begin{split}R(0 \rightarrow t_{2}) \times R(t_{1} \rightarrow 0) &= R(t_{1} \rightarrow t_{2}) \times R(0 \rightarrow t_{1}) \times R(t_{1} \rightarrow 0) \\ R(0 \rightarrow t_{2}) \times R(t_{1} \rightarrow 0) &= R(t_{1} \rightarrow t_{2}) \\ R(t_{1} \rightarrow t_{2}) &= R(0 \rightarrow t_{2}) \times R(t_{1} \rightarrow 0)\end{split}\]

The plate circuit path rotation from anchor plate \(P_{A}\) to moving plate \(P_{M}\) (via fixed plate \(P_{F}\)) is given by:

\[R(P_{A} \rightarrow P_{M}) = R(P_{A} \rightarrow P_{F}) \times R(P_{F} \rightarrow P_{M})\]

…or by pre-multiplying both sides by \(R(P_{F} \rightarrow P_{A})\) this becomes…

\[\begin{split}R(P_{F} \rightarrow P_{A}) \times R(P_{A} \rightarrow P_{M}) &= R(P_{F} \rightarrow P_{A}) \times R(P_{A} \rightarrow P_{F}) \times R(P_{F} \rightarrow P_{M}) \\ R(P_{F} \rightarrow P_{A}) \times R(P_{A} \rightarrow P_{M}) &= R(P_{F} \rightarrow P_{M}) \\ R(P_{F} \rightarrow P_{M}) &= R(P_{F} \rightarrow P_{A}) \times R(P_{A} \rightarrow P_{M})\end{split}\]

Note that the rotations for relative times and for relative plates have the opposite order of each other !

In other words:

  • For times \(0 \rightarrow t_{1} \rightarrow t_{2}\) you apply the \(0 \rightarrow t_{1}\) rotation first followed by the \(t_{1} \rightarrow t_{2}\) rotation:

    \[R(0 \rightarrow t_{2}) = R(t_{1} \rightarrow t_{2}) \times R(0 \rightarrow t_{1})\]

  • For plate circuit \(P_{A} \rightarrow P_{F} \rightarrow P_{M}\) you apply the \(P_{F} \rightarrow P_{M}\) rotation first followed by the \(P_{A} \rightarrow P_{F}\) rotation:

    \[R(P_{A} \rightarrow P_{M}) = R(P_{A} \rightarrow P_{F}) \times R(P_{F} \rightarrow P_{M})\]

    Note

    This is not \(P_{A} \rightarrow P_{F}\) followed by \(P_{F} \rightarrow P_{M}\) as you might expect (looking at the time example).

This is probably best explained by the difference between thinking in terms of the grand fixed coordinate system and local coordinate system (see http://glprogramming.com/red/chapter03.html#name2). Essentially, in the plate circuit \(P_{A} \rightarrow P_{F} \rightarrow P_{M}\), the \(P_{F} \rightarrow P_{M}\) rotation can be thought of as a rotation within the local coordinate system of \(P_{A} \rightarrow P_{F}\). In other words \(P_{F} \rightarrow P_{M}\) is not a rotation that occurs relative to the global spin axis but a rotation relative to the local coordinate system of plate \(P_{F}\) after it has been rotated relative to the anchor plate \(P_{A}\).

For the times \(0 \rightarrow t_{1} \rightarrow t_{2}\) this local/relative coordinate system concept does not apply.

Note that a rotation must be relative to present day (0Ma) before it can be separated into a (plate circuit) chain of moving/fixed plate pairs. Hence \(R(t_{1} \rightarrow t_{2},P_{A} \rightarrow P_{C}) \neq R(t_{1} \rightarrow t_{2},P_{A} \rightarrow P_{B}) \times R(t_{1} \rightarrow t_{2},P_{B} \rightarrow P_{C})\) demonstrates this mistake.

The following shows the correct way to separate \(P_{A} \rightarrow P_{C}\) into the (plate circuit) chain of moving/fixed plate pairs \(P_{A} \rightarrow P_{B}\) and \(P_{B} \rightarrow P_{C}\)…

\[\begin{split}R(t_{1} \rightarrow t_{2},P_{A} \rightarrow P_{C}) \\ & = R(0 \rightarrow t_{2},P_{A} \rightarrow P_{C}) \times R(t_{1} \rightarrow 0,P_{A} \rightarrow P_{C}) \\ & = R(0 \rightarrow t_{2},P_{A} \rightarrow P_{C}) \times R(0 \rightarrow t_{1},P_{A} \rightarrow P_{C})^{-1} \\ & \text{// Now that all times are relative to 0Ma we can split } P_{A} \rightarrow P_{C} \text{ into } P_{A} \rightarrow P_{B} \rightarrow P_{C} \text{ ...} \\ & = R(0 \rightarrow t_{2},P_{A} \rightarrow P_{B}) \times R(0 \rightarrow t_{2},P_{B} \rightarrow P_{C}) \times [R(0 \rightarrow t_{1},P_{A} \rightarrow P_{B}) \times R(0 \rightarrow t_{1},P_{B} \rightarrow P_{C})]^{-1} \\ & = R(0 \rightarrow t_{2},P_{A} \rightarrow P_{B}) \times R(0 \rightarrow t_{2},P_{B} \rightarrow P_{C}) \times R(0 \rightarrow t_{1},P_{B} \rightarrow P_{C})^{-1} \times R(0 \rightarrow t_{1},P_{A} \rightarrow P_{B})^{-1}\end{split}\]

…where \(P_{A} \rightarrow P_{B} \rightarrow P_{C}\) means \(P_{B} \rightarrow P_{C}\) is the rotation of \(P_{C}\) relative to \(P_{B}\) and \(P_{A} \rightarrow P_{B}\) is the rotation of \(P_{B}\) relative to \(P_{A}\). The need for rotation \(P_{A} \rightarrow P_{C}\) to be relative to present day (0Ma) before it can be split into \(P_{A} \rightarrow P_{B}\) and \(P_{B} \rightarrow P_{C}\) is because \(P_{A} \rightarrow P_{B}\) and \(P_{B} \rightarrow P_{C}\) are defined (in the rotation file) as total reconstruction poles which are always relative to present day.

Note

The inverse of rotation \(R\) is denoted \(R^{-1}\).
Such that \(R \times R^{-1} = R^{-1} \times R = I\) where \(I\) is the identify rotation.

Equivalent total rotation

The equivalent total rotation of moving plate \(P_{M}\) relative to anchor plate \(P_{A}\), and from present day time \(0\) to time \(t_{to}\) is:

\[R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M})\]

In pyGPlates, the equivalent total rotation can be obtained pygplates.RotationModel.get_rotation() as:

rotation_model = pygplates.RotationModel(...)
...
equivalent_total_rotation = rotation_model.get_rotation(to_time, moving_plate)

Relative total rotation

The relative total rotation of moving plate \(P_{M}\) relative to fixed plate \(P_{F}\), and from present day time \(0\) to time \(t_{to}\) is:

\[\begin{split}R(0 \rightarrow t_{to},P_{F} \rightarrow P_{M}) \\ & = R(0 \rightarrow t_{to},P_{F} \rightarrow P_{A}) \times R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M}) \\ & = R(0 \rightarrow t_{to},P_{A} \rightarrow P_{F})^{-1} \times R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M})\end{split}\]

…where \(P_{A}\) is the anchor plate.

In pyGPlates, the relative total rotation can be obtained from pygplates.RotationModel.get_rotation() as:

rotation_model = pygplates.RotationModel(...)
...
relative_total_rotation = rotation_model.get_rotation(to_time, moving_plate, fixed_plate_id=fixed_plate)

Equivalent stage rotation

The equivalent stage rotation of moving plate \(P_{M}\) relative to anchor plate \(P_{A}\), and from time \(t_{from}\) to time \(t_{to}\) is:

\[\begin{split}R(t_{from} \rightarrow t_{to},P_{A} \rightarrow P_{M}) \\ & = R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M}) \times R(t_{from} \rightarrow 0,P_{A} \rightarrow P_{M}) \\ & = R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M}) \times R(0 \rightarrow t_{from},P_{A} \rightarrow P_{M})^{-1}\end{split}\]

In pyGPlates, the equivalent stage rotation can be obtained pygplates.RotationModel.get_rotation() as:

rotation_model = pygplates.RotationModel(...)
...
equivalent_stage_rotation = rotation_model.get_rotation(to_time, moving_plate, from_time)

Relative stage rotation

The relative stage rotation of moving plate \(P_{M}\) relative to fixed plate \(P_{F}\), and from time \(t_{from}\) to time \(t_{to}\) is:

\[\begin{split}R(t_{from} \rightarrow t_{to},P_{F} \rightarrow P_{M}) \\ & = R(0 \rightarrow t_{to},P_{F} \rightarrow P_{M}) \times R(t_{from} \rightarrow 0,P_{F} \rightarrow P_{M}) \\ & = R(0 \rightarrow t_{to},P_{F} \rightarrow P_{M}) \times R(0 \rightarrow t_{from},P_{F} \rightarrow P_{M})^{-1} \\ & = R(0 \rightarrow t_{to},P_{F} \rightarrow P_{A}) \times R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M}) \times [R(0 \rightarrow t_{from},P_{F} \rightarrow P_{A}) \times R(0 \rightarrow t_{from},P_{A} \rightarrow P_{M})]^{-1} \\ & = R(0 \rightarrow t_{to},P_{A} \rightarrow P_{F})^{-1} \times R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M}) \times [R(0 \rightarrow t_{from},P_{A} \rightarrow P_{F})^{-1} \times R(0 \rightarrow t_{from},P_{A} \rightarrow P_{M})]^{-1} \\ & = R(0 \rightarrow t_{to},P_{A} \rightarrow P_{F})^{-1} \times R(0 \rightarrow t_{to},P_{A} \rightarrow P_{M}) \times R(0 \rightarrow t_{from},P_{A} \rightarrow P_{M})^{-1} \times R(0 \rightarrow t_{from},P_{A} \rightarrow P_{F})\end{split}\]

…where \(P_{A}\) is the anchor plate.

In pyGPlates, the relative stage rotation can be obtained pygplates.RotationModel.get_rotation() as:

rotation_model = pygplates.RotationModel(...)
...
relative_stage_rotation = rotation_model.get_rotation(to_time, moving_plate, from_time, fixed_plate)

Topologies

This section covers topologies in pyGPlates.

Topological model

A topological model is represented by a pygplates.TopologicalModel. It can be created from topological features (in files, features or feature collections) and a rotation model (created from rotation files, features or feature collections):

rotation_model = pygplates.RotationModel('rotations.rot')
topological_model = pygplates.TopologicalModel('topologies.gpml', rotation_model)

Note

Alternatively you can just pass the rotation filenames (or features) directly into the topological model:

topological_model = pygplates.TopologicalModel('topologies.gpml', 'rotations.rot')

You can also control how topologies are resolved using pygplates.ResolveTopologyParameters - currently these parameters only affect deforming networks. This is done by specifying the default_resolve_topology_parameters - see Strain rate clamping, Strain rate smoothing and Exponential rift stretching profile for more details.

Note

You can also override the default parameters for each topological entry (eg, each file, feature collection or feature) by specifying a 2-tuple (topological entry, pygplates.ResolveTopologyParameters) instead of just the topological entry.

A topological model can:

Topological snapshot

A topological snapshot is represented by a pygplates.TopologicalSnapshot. It can be created by resolving a pygplates.TopologicalModel to a specific reconstruction time. For example, to create a topological snapshot for each reconstruction time from 0 to 1000Ma in 1Myr increments:

for reconstruction_time in range(1000):
   topological_snapshot = topological_model.topological_snapshot(reconstruction_time)

Alternatively, a topological snapshot can be created directly from topological features and a rotation model (similar to how a topological model is created) and a reconstruction time:

for reconstruction_time in range(1000):
   topological_snapshot = pygplates.TopologicalSnapshot('topologies.gpml', rotation_model, reconstruction_time)

Note

It is more efficient to generate snapshots from a pygplates.TopologicalModel (rather than explicity using pygplates.TopologicalSnapshot(...)). This is because a topological model only needs to read/parse the input topological and rotation features once, rather than at each time step. And also, the topological snapshots are cached internally within the topological model, so requesting the same snapshot again (at the same reconstruction time) will not require the topologies to be resolved again (at that reconstruction time).

A topological snapshot can:

Plate boundary statistics

Note

The following sample codes use plate boundary statistics:

Statistics at uniformly spaced points along plate boundaries can be generated from a topological snapshot using pygplates.TopologicalSnapshot.calculate_plate_boundary_statistics(). For example, to generate statistics at points spaced 1 degree apart (along all plate boundaries):

uniform_point_spacing_radians = math.radians(1)
plate_boundary_stats = topological_snapshot.calculate_plate_boundary_statistics(uniform_point_spacing_radians)

You can also restrict which plate boundaries to generate points along. For example, to generate points only along subduction zones and mid-ocean ridges:

plate_boundary_stats = topological_snapshot.calculate_plate_boundary_statistics(
      uniform_point_spacing_radians,
      boundary_section_filter = [pygplates.FeatureType.gpml_subduction_zone,
                                 pygplates.FeatureType.gpml_mid_ocean_ridge])

…or even define your own criteria as a filter function accepting a single argument of type pygplates.ResolvedTopologicalSection and returning True if uniform points should be generated along that boundary section. For example, the equivalent of the above example (generating points only along subduction zones and mid-ocean ridges) would be:

def boundary_section_filter_function(resolved_topological_section):
   feature_type = resolved_topological_section.get_feature().get_feature_type()
   return (feature_type == pygplates.FeatureType.gpml_subduction_zone or
           feature_type == pygplates.FeatureType.gpml_mid_ocean_ridge)

plate_boundary_stats = topological_snapshot.calculate_plate_boundary_statistics(
      uniform_point_spacing_radians,
      boundary_section_filter = boundary_section_filter_function)

Note

You can also group uniform points with the shared sub-segment they came from by setting return_shared_sub_segment_dict to True.

Each point gets its own statistic represented by a pygplates.PlateBoundaryStatistic. For example, to query the uniformly spaced point locations and their convergence velocity magnitudes and obliquities:

for stat in plate_boundary_stats:
   boundary_point = stat.boundary_point
   if convergence_velocity is not None:  # make sure the left and right plates exist
      convergence_velocity_magnitude = stat.convergence_velocity_magnitude
      convergence_velocity_obliquity = stat.convergence_velocity_obliquity

There are many other statistics such as plate boundary velocity, plate boundary normal direction, left and right plate velocities, left and right plate identifiers (ie, which plate, or deforming network, is left and right of the point) and distance to the ends of the boundary section (containing the point).

Topologically reconstruct geometries

Note

The following sample codes use topological reconstruction:

Usually features are reconstructed using pygplates.ReconstructModel, which relies only on the properties of the features (such as their reconstruction plate IDs) to reconstruct them to past geological times.

An alternative approach is to use topologies (topological closed plate polygons and networks) to reconstruct an initial geometry. In this case it is the topological plates and networks that determine how the geometry moves over time. In other words, the geometry rigidly rotates when it is in rigid plates and deforms when it is in deforming networks.

What is topological reconstruction?

Topological reconstruction is an incremental process whereby each point in an initial geometry is reconstructed over a time period by dividing that time period into a series of smaller time intervals. Within each time interval, the geometry at the start of the interval is reconstructed to the end of the interval using the resolved topologies (at the start of the interval). This incremental reconstruction is performed iteratively over the full time period to obtain a history of reconstruction snapshots (of the geometry), with each snapshot occupying a time slot.

For each new time interval, the resolved topologies can change, such as plates splitting/merging and deforming networks appearing/disappearing. So at the start of each time interval, each point of the geometry is tested to see which topological plate or network it lies within (with higher priority given to networks since they typically overlay the rigid plates). Then each point is reconstructed over the time interval using the topological plate (see pygplates.ResolvedTopologicalBoundary.reconstruct_point()) or topological network (see pygplates.ResolvedTopologicalNetwork.reconstruct_point()) that the point lies within.

Reconstruction plate ID

Since topological reconstruction is peformed using topologies, no feature properties are needed (in contrast with non-topological reconstruction using pygplates.ReconstructModel). However, if a geometry point does not intersect any resolved topologies during a time interval then an optional reconstruction plate ID is used to rigidly reconstruct it over that time interval. And if a reconstruction plate ID was not provided then the point does not move over that time interval.

Note

Some geometry points can fail to intersect topologies if the topologies are regional (instead of global), or if there are cracks between adjacent topologies (due to the way they were built).

Deactivating points

The history of reconstruction snapshots covers a time range from an oldest time to a youngest time. And the initial geometry is provided at an initial time (that can be inside or outside that time range). Hence an initial geometry can be topologically reconstructed forward in time, or backward in time, or both, depending on where the initial time is in relation to the oldest and youngest times.

Initially all geometry points are active at the initial time, but can get progressively deactivated as they are topologically reconstructed away from the initial time. When a point is deactivated it becomes inactive and is no longer topologically reconstructed for subsequent time slots (further from the initial time). When reconstructed forward in time, points on oceanic crust get deactivated as they are subducted. And when reconstructed backward in time, they get deactivated as they reach their time of appearance (at a mid-ocean ridge).

Using topological reconstruction

Topological reconstruction requires a pygplates.TopologicalModel and a geometry. Currently the geometry can only be one or more points. Then pygplates.TopologicalModel.reconstruct_geometry() can be used to generate a reconstructed history of snapshots of the geometry points, and associated quantities (like velocity), that are stored in the returned pygplates.ReconstructedGeometryTimeSpan. For example, to topologically reconstruct points from their initial positions at 100 Ma to present day, in increments of 1 Myr:

# Convert from latitudes and longitudes to a list of pygplates.PointOnSphere.
lats = [...]  # point latitudes
lons = [...]  # point longitudes
points = [pygplates.PointOnSphere(lat, lon) for lat, lon in zip(lats, lons)]

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      points,
      initial_time=100)

The returned pygplates.ReconstructedGeometryTimeSpan contains 101 reconstructed snapshots of the initial geometry in its history. You can use it to query the reconstructed geometry at any reconstruction time. For example, to query the reconstructed points at 50 Ma:

reconstructed_points = reconstructed_geometry_time_span.get_geometry_points(50)

if reconstructed_points:
   # Convert from a list of pygplates.PointOnSphere to a list of (latitude, longitude) tuples.
   reconstructed_lat_lons = [point.to_lat_lon() for point in reconstructed_points]

See also

Reconstructed geometry time span for more details on querying reconstruction snapshots.

Time spans

The time span of snapshots is determined by the oldest and youngest times.

In the above example, points were reconstructed forward in time (from 100 Ma to present day). So the oldest time was 100 Ma and the youngest was 0 Ma.

You can also reconstruct backward in time. For example, to reconstruct from present day to 100 Ma, in increments of 1 Myr:

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      points,
      initial_time=0,
      oldest_time=100)

…where we needed to explicitly specify oldest_time because otherwise it defaults to initial_time (which in this example is present day).

Note

Even though the reconstruction is backward in time, the oldest and youngest times are still 100 Ma and 0 Ma, respectively.

In the above cases, the youngest time defaults to present day. However you can explicitly set it using the youngest_time argument. For example, if you only want a history of snapshots from 100 Ma to 50 Ma (instead of 100 Ma to present day):

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      points,
      initial_time=0,
      oldest_time=100,
      youngest_time=50)

It’s also possible to reconstruct both forward and backward in time. This happens when the initial time is between the oldest and youngest times. For example, if the initial points are at 50 Ma but you want a time range of snapshots from 100 Ma to present day:

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      points,
      initial_time=50,
      oldest_time=100)

In this case, the initial points are reconstructed both forward in time from 50 Ma to present day and backward in time from 50 Ma to 100 Ma (in order to generate all snapshots from 100 Ma to present day).

You can also choose the time interval between reconstruction snapshots using the time_increment argument (which defaults to 1 Myr). The time increment, along with the oldest and youngest times, determine the time slots.

Note

oldest_time - youngest_time must be an integer multiple of time_increment.

If you choose a large time increment then the snapshots will be spaced farther apart and the resulting reconstruction accuracy will suffer. Another source of inaccuracy is due to the initial time of the initial geometry being internally snapped to the nearest time slot. For these reasons the time increment defaults to 1 Myr (which is typically the smallest time resolution used in topological models).

Reconstruction plate ID

In the above cases, the geometry is already in the correct position at the initial time. In other words, the geometry is a snapshot at the initial time. For example, it could be uniform points spread across the entire globe at the initial time (and we want to see where they end up at other times). So we did not specify the reconstruction_plate_id argument.

However if the geometry is a present day geometry localised to a specific plate (and the initial time is in the past) then specifying a reconstruction plate ID will reconstruct it to the initial time (to become the snapshot at the initial time, before topologically reconstruction into the other snapshots proceeds). For example, if the geometry represents its present day position on plate 701 (and we’re reconstructing forward in time from 100 Ma to present day) then:

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      points_at_present_day,
      initial_time=100,
      reconstruction_plate_id=701)

…will first rigidly reconstruct points_at_present_day from present day to 100 Ma using plate 701, and then topologically reconstruct them from 100 Ma to present day (generating snapshots at 1 Myr intervals).

Note

reconstruction_plate_id also has other purposes. For example, when generating the history of snapshots and when querying geometry points.

Deactivating points

By default, geometry points can get progressively deactivated when they are topologically reconstructed away from the initial time. This is useful for points on oceanic crust because that crust can get subducted, and it is typically younger than continental crust. Therefore, oceanic points will get deactivated as they are subducted going forward in time and deactivated as they reach their time of appearance (at mid-ocean ridges) going backward in time. This is the default behaviour and works for both oceanic and continental crust.

To disable this ability you can explicitly set the deactivate_points argument to None. Then the points will always remain active. This can be used (but is not necessary) when the points are all within the interior of continents (where crust exists at present day and has existed for a long time). For example, to reconstruct continental points forward in time from 100 Ma to present day (without attempting to deactivate any):

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      points,
      initial_time=100,
      deactivate_points=None)

You can also change how points are deactivated, by either:

  • changing the parameters of the default deactivation algorithm, or

  • implementing your own deactivation algorithm.

The default deactivation algorithm is implemented in pygplates.ReconstructedGeometryTimeSpan.DefaultDeactivatePoints.

To use the default parameters of the default deactivation algorithm you don’t need to specify the deactivate_points argument. For example, you can just call:

topological_model.reconstruct_geometry(
      points,
      initial_time=100)

…since that is equivalent to calling:

topological_model.reconstruct_geometry(
      points,
      initial_time=100,
      deactivate_points=pygplates.ReconstructedGeometryTimeSpan.DefaultDeactivatePoints())

However, you can change the parameters of the default deactivation algorithm. For example, when reconstructing oceanic points (forward in time from 100 Ma to present day):

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      points,
      initial_time=100,
      deactivate_points=pygplates.ReconstructedGeometryTimeSpan.DefaultDeactivatePoints(
            # Choose our own parameters that are different than the defaults...
            threshold_velocity_delta = 0.9, # cms/yr
            threshold_distance_to_boundary = 15, # kms/myr
            deactivate_points_that_fall_outside_a_network = True))

You can also implement your own deactivation algorithm by implementing your own class that inherits from pygplates.ReconstructedGeometryTimeSpan.DeactivatePoints and overrides its deactivate method.

Note

This is what the default deactivation algorithm does. In other words, the DefaultDeactivatePoints class inherits from the DeactivatePoints class.

See also

pygplates.ReconstructedGeometryTimeSpan.DeactivatePoints for more details.

Reconstructed geometry time span

A pygplates.ReconstructedGeometryTimeSpan contains a history of reconstruction snapshots generated by pygplates.TopologicalModel.reconstruct_geometry().

Each snapshot stores the following quantities:

The history of snapshots is stored in time slots defined by pygplates.ReconstructedGeometryTimeSpan.get_time_span() whose time range is determined by the oldest_time and youngest_time arguments of pygplates.TopologicalModel.reconstruct_geometry(). For example, to iterate over the stored history of reconstructed geometry points (from oldest time to youngest time):

oldest_time, youngest_time, time_increment, num_time_slots = reconstructed_geometry_time_span.get_time_span()
for time_slot in range(num_time_slots):
   reconstruction_time = oldest_time - time_slot * time_increment
   reconstructed_points = reconstructed_geometry_time_span.get_geometry_points(reconstruction_time)

However, you can query the snapshots at any arbitrary reconstruction time, it does not have to match a time slot. And it can be outside the time range of snapshots (although typically you would generate a time range that contains all desired reconstruction times). For times not matching a time slot, the behaviour is defined separately for each snapshot quantity.

For example, to iterate over the reconstructed geometry points at 1Myr intervals (from oldest time to youngest time) regardless of the time slot intervals (which could be larger than 1Myr):

oldest_time, youngest_time, _, _ = reconstructed_geometry_time_span.get_time_span()
reconstruction_time = oldest_time
while reconstruction_time >= youngest_time:
   reconstructed_points = reconstructed_geometry_time_span.get_geometry_points(reconstruction_time)
   reconstruction_time -= 1.0

When querying the various quantities in a snapshot (such as points or their velocities), each query has a return_inactive_points argument. It defaults to False so that only quantities associated with active points are returned. However, if you set it to True then quantities associated with both active and inactive points are returned. Each inactive point will have a value of None (since quantities cannot be calculated at inactive points). This can be useful when you need to keep track of points and their quantities over time, since you can use point indices (an integer index into an array of points) which is not possible otherwise. For example, to find the maximum velocity of each point (in a geometry) over the time range of the snapshots:

import numpy as np

# The number of initial points in the geometry (initially all points are active).
num_initial_points = len(initial_points)

# A NumPy array of zeros (one for each point).
# This will later get updated with the max velocity of each point (in the same order as the points).
max_point_velocities = np.zeros(num_initial_points)

# Topologically reconstruct the initial points from 100 Ma to present day (at 1 Myr intervals).
reconstructed_geometry_time_span = topological_model.reconstruct_geometry(initial_points, initial_time=100)

# Iterate over the time slots (100, 99, ..., 1, 0 Ma).
oldest_time, youngest_time, time_increment, num_time_slots = reconstructed_geometry_time_span.get_time_span()
for time_slot in range(num_time_slots):
   reconstruction_time = oldest_time - time_slot * time_increment

   # Get the velocity at each point (for each inactive point it will be 'None').
   reconstructed_velocities = reconstructed_geometry_time_span.get_velocities(
         reconstruction_time,
         return_inactive_points=True)

   # If all points are inactive (in the current time slot) then 'reconstructed_velocities' itself will be 'None'.
   #
   # Note: If it is 'None' then you could potentially finish here (because once all points are deactivated
   #       they can't be reactivated). However this depends on the order you visit the time slots. It's only
   #       possible if you start at the initial time (slot) which in our case happens to be the oldest time
   #       (since we're reconstructing *forward* in time from 100 Ma to present day).
   if reconstructed_velocities:
      # Iterate over all the points (some might be inactive).
      for point_index in range(num_initial_points):
         velocity = reconstructed_velocities[point_index]
         # If the current point is active (in the current time slot) then it will have a velocity.
         if velocity is not None:
            # See if velocity is the maximum for the current point over all time slots visited so far.
            velocity_magnitude = velocity.get_magnitude()
            if velocity_magnitude > max_point_velocities[point_index]:
               max_point_velocities[point_index] = velocity_magnitude

# Print out the maximum velocity of each geometry point.
for point_index in range(num_initial_points):
   lat, lon = initial_points[point_index].to_lat_lon()
   velocity_magnitude = max_point_velocities[point_index]
   print('Max velocity of point initially at lon/lat ({}, {}) is {} km/myr'.format(lon, lat, velocity_magnitude))

…where we’ve associated a (maximum) velocity with each initial geometry point (such that the maximum velocity, and initial position, of any geometry point can be found using its point_index).

Geometry points

The reconstructed geometry points at a reconstruction time can be queried using pygplates.ReconstructedGeometryTimeSpan.get_geometry_points():

reconstructed_points = reconstructed_geometry_time_span.get_geometry_points(reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_points:
   ...

If the requested reconstruction time matches a time slot in the time span then the geometry points of the snapshot in that time slot are returned.

If the requested reconstruction time is within the time range of the snapshots, but does not match a time slot, then the geometry points in the time slot (of the two time slots nearest the reconstruction time) that is closest to the initial time (specified in pygplates.TopologicalModel.reconstruct_geometry()) will be incrementally reconstructed (away from the initial time) to the requested reconstruction time using pygplates.ResolvedTopologicalBoundary.reconstruct_point() or pygplates.ResolvedTopologicalNetwork.reconstruct_point() (depending on which plate/network in the time slot each active point lies within). And those reconstructed points will be returned.

Note

The returned geometry points will have the same active status as the time slot they’re incrementally reconstructed from. In other words, if a point is active in the source time slot then it’ll also be active in the returned geometry points.

If the requested reconstruction time is outside the time range of the snapshots then the reconstruction plate ID specified in pygplates.TopologicalModel.reconstruct_geometry() will be used to rigidly reconstruct the geometry points from the oldest time slot (if the requested reconstruction time is older), or from the youngest time slot (if the requested reconstruction time is younger), to the requested reconstruction time. And those reconstructed points will be returned.

Note

The active status of the returned points will be the same as those in the oldest or youngest time slot. Which means there can still be active geometry points when the reconstruction time is outside the time range of the snapshots.

Note

If no reconstruction plate ID was specified then there will be no rigid rotation, and so the geometry points from the oldest or youngest time slot will effectively be returned. However typically you would generate a time range that contains all desired reconstruction times (so this situation would not typically occur).

Note

The reconstruction plate ID can also be used when the requested reconstruction time is inside the time range and some geometry points are outside all resolved topologies (and hence cannot be reconstructed by the topologies). This can happen if the topologies are regional (instead of global) or if there are cracks between adjacent topologies (due to the way they were built).

In all cases, if none of the geometry points are active at the reconstruction time then None will be returned.

Topology locations

A topology location identifies the resolved topology boundary or network that contains a reconstructed geometry point, or identifies no resolved topologies if the point does not intersect any.

The topology location of each reconstructed geometry point at a reconstruction time can be queried using pygplates.ReconstructedGeometryTimeSpan.get_topology_point_locations():

reconstructed_topology_locations = reconstructed_geometry_time_span.get_topology_point_locations(reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_topology_locations:
   ...

A topology location is returned for each geometry point that is active at the requested reconstruction time (see Geometry points). If none of the points are active then None will be returned.

If the requested reconstruction time is within the time range of the snapshots then the returned topology locations are those of the geometry points in the time slot (of the two time slots nearest the reconstruction time) that is closest to the initial time (specified in pygplates.TopologicalModel.reconstruct_geometry()).

Note

The topology locations are at the time of the time slot (rather than the reconstruction time) because topologies are only resolved at the time slots.

If the requested reconstruction time is outside the time range of the snapshots then the returned topology locations identify no resolved topologies. In other words, pygplates.TopologyPointLocation.not_located_in_resolved_topology() will return True for each geometry point. This is because topologies are not resolved outside the time range.

See also

pygplates.ResolvedTopologicalBoundary.get_point_location() and pygplates.ResolvedTopologicalNetwork.get_point_location()

Velocities

The velocities of reconstructed geometry points at a reconstruction time can be queried using pygplates.ReconstructedGeometryTimeSpan.get_velocities():

reconstructed_velocities = reconstructed_geometry_time_span.get_velocities(reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_velocities:
   ...

A velocity is calculated for each geometry point that is active at the requested reconstruction time (see Geometry points). If none of the points are active then None will be returned.

If the requested reconstruction time is within the time range of the snapshots then the returned velocities are calculated at the geometry points in the time slot (of the two time slots nearest the reconstruction time) that is closest to the initial time (specified in pygplates.TopologicalModel.reconstruct_geometry()).

Note

The velocities are calculated at the time of the time slot (rather than the reconstruction time), and at the positions of the active geometry points in the time slot (rather than the geometry points at the reconstruction time - see Geometry points). So, this is more like a nearest neighbour interpolation (rather than a linear interpolation) of the two nearest time slots. This is done since velocities are calculated using topologies, which are only resolved at the time slots, and the active status of velocities needs to be synchronised with the geometry points.

The velocities are determined by the topologies (rigid plates and deforming networks) resolved at the time of the time slot using pygplates.ResolvedTopologicalBoundary.get_point_velocity() or pygplates.ResolvedTopologicalNetwork.get_point_velocity() (depending on which plate/network in the time slot each active point lies within).

If the requested reconstruction time is outside the time range of the snapshots then the returned velocities are determined by the reconstruction plate ID specified in pygplates.TopologicalModel.reconstruct_geometry(), and they’re calculated at the positions of the active geometry points at the reconstruction time (see Geometry points).

Note

If no reconstruction plate ID was specified then the velocities will be zero.

Note

The reconstruction plate ID can also be used when the requested reconstruction time is inside the time range and some geometry points are outside all resolved topologies (and hence their velocities cannot be determined by the topologies). This can happen if the topologies are regional (instead of global) or if there are cracks between adjacent topologies (due to the way they were built).

Strain rates

The strain rates of reconstructed geometry points at a reconstruction time can be queried using pygplates.ReconstructedGeometryTimeSpan.get_strain_rates():

reconstructed_strain_rates = reconstructed_geometry_time_span.get_strain_rates(reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_strain_rates:
   ...

A strain rate is returned for each geometry point that is active at the requested reconstruction time (see Geometry points). If none of the points are active then None will be returned.

If the requested reconstruction time is within the time range of the snapshots then the returned strain rates are interpolated between the two time slots nearest the reconstruction time.

Note

The time slot further from the initial time (specified in pygplates.TopologicalModel.reconstruct_geometry()) might have deactivated some points from the time slot closer to the initial time (see Deactivating points). For these points the strain rate is not interpolated (instead it’s obtained from the time slot closer to the initial time).

The strain rates in time slots are determined by the topologies (rigid plates and deforming networks) resolved at the time of the time slot using pygplates.ResolvedTopologicalBoundary.get_point_strain_rate() or pygplates.ResolvedTopologicalNetwork.get_point_strain_rate() (depending on which plate/network in the time slot each active point lies within). And the strain rate will be zero for each geometry point (in a time slot) that is not within a deforming network.

If the requested reconstruction time is outside the time range of the snapshots then the returned strain rates will be zero (no deformation).

Strains

The strains of reconstructed geometry points at a reconstruction time can be queried using pygplates.ReconstructedGeometryTimeSpan.get_strains():

reconstructed_strains = reconstructed_geometry_time_span.get_strains(reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_strains:
   ...

A strain is returned for each geometry point that is active at the requested reconstruction time (see Geometry points). If none of the points are active then None will be returned.

If the requested reconstruction time is within the time range of the snapshots then the returned strains are interpolated between the two time slots nearest the reconstruction time.

Note

The time slot further from the initial time (specified in pygplates.TopologicalModel.reconstruct_geometry()) might have deactivated some points from the time slot closer to the initial time (see Deactivating points). For these points the strain is not interpolated (instead it’s obtained from the time slot closer to the initial time).

The strain of each geometry point is generated (in the time slots) by accumulating its strain rates forward in time, over the time range of the snapshots, using pygplates.Strain.accumulate(). The initial strain of each active geometry point in the oldest time slot will be the identity strain (since deformation has not yet occurred). And the accumulated strain of a geometry point will only change (going forward in time) if the point undergoes deformation (ie, is in a deforming network in one or more time slots).

If the requested reconstruction time is outside the time range of the snapshots then the returned strains will be identity strains (no deformation) if the requested reconstruction time is older than the oldest time slot, and will be the accumulated strains of the youngest time slot if the requested reconstruction time is younger than the youngest time slot (since strains do not accumulate outside the time range of the snapshots because strain rates are zero there).

Scalar values

Each geometry point can have one or more scalar values. And each scalar value (per point) is associated with a scalar type.

Each scalar type belongs to one of two categories:

  • Built-in scalar types: whose scalar values change over time due to deformation

    These are:

    Scalar values for these scalar types are always available.

    And their initial scalar values have default values (at the initial time). Hence the initial_scalars argument of pygplates.TopologicalModel.reconstruct_geometry() does not need to be specified.

  • User-defined scalar types: whose scalar values are constant over time

    Note

    Even though these scalar values are constant (over time) they still get deactivated when their associated geometry points get deactivated.

    These can be any pygplates.ScalarType that you define. They are simply a way to associate your own data with the reconstructed geometry points.

    Scalar values for these scalar types are only available if you define them (using the initial_scalars argument of pygplates.TopologicalModel.reconstruct_geometry()). For example:

    # Define your own scalar types.
my_scalar_type_0 = pygplates.ScalarType.create_gpml('MyScalarType_0')
my_scalar_type_1 = pygplates.ScalarType.create_gpml('MyScalarType_1')

# Define associated scalar values (one per geometry point per scalar type).
my_scalar_type_0_values = [...]
my_scalar_type_1_values = [...]

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      initial_points,
      initial_time = 100,
      # dict with two entries (each entry mapping a scalar type to its scalar values)...
      initial_scalars = { my_scalar_type_0 : my_scalar_type_0_values, my_scalar_type_1 : my_scalar_type_1_values })

    Note

    The built-in scalar types are still available when user-defined scalar types are defined.

The scalar values of each reconstructed geometry point at a reconstruction time can be queried using pygplates.ReconstructedGeometryTimeSpan.get_scalar_values(). By default this will return a dict mapping all scalar types (built-in and any user-defined) to their scalar values. For example:

# Get all active scalar values (associated with all built-in and user-defined scalar types).
active_scalar_values = reconstructed_geometry_time_span.get_scalar_values(reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if active_scalar_values:

   # Extract the scalar values associated with the built-in scalar types.
   crustal_thicknesses_in_kms = active_scalar_values[pygplates.ScalarType.gpml_crustal_thickness]
   crustal_stretching_factors = active_scalar_values[pygplates.ScalarType.gpml_crustal_stretching_factor]
   crustal_thinning_factors = active_scalar_values[pygplates.ScalarType.gpml_crustal_thinning_factor]
   tectonic_subsidences = active_scalar_values[pygplates.ScalarType.gpml_tectonic_subsidence]

   # Extract the scalar values associated with the user-defined scalar types.
   my_active_scalar_values_0 = active_scalar_values[my_scalar_type_0]
   my_active_scalar_values_1 = active_scalar_values[my_scalar_type_1]

Note

Alternatively, you can specify a scalar type directly to pygplates.ReconstructedGeometryTimeSpan.get_scalar_values(). For example:

my_active_scalar_values_0 = reconstructed_geometry_time_span.get_scalar_values(
      reconstruction_time,
      my_scalar_type_0)

A scalar value (per scalar type) is returned for each geometry point that is active at the requested reconstruction time (see Geometry points). If none of the points are active then None will be returned.

If the requested reconstruction time is within the time range of the snapshots then the returned scalar values are those of the geometry points in the time slot (of the two time slots nearest the reconstruction time) that is closest to the initial time (specified in pygplates.TopologicalModel.reconstruct_geometry()).

Note

This is at the time of the time slot (rather than the reconstruction time), so this is more like a nearest neighbour interpolation (rather than a linear interpolation) of the two nearest time slots. This only matters for built-in scalar types since user-defined scalar types are constant over time.

If the requested reconstruction time is outside the time range of the snapshots then the returned scalar values will be from the oldest time slot (if the requested reconstruction time is older) or from the youngest time slot (if the requested reconstruction time is younger).

Crustal thickness factors

The crustal thickness factor \(F(t) = \frac{T(t)}{T(t_{initial})}\) measures the ratio of the crustal thickness at a reconstruction time \(T(t)\) to the initial crustal thickness at the initial time \(T(t_{initial})\). It is only calculated internally, and always has a value of 1.0 at the initial time (\(F(t_{initial}) = 1.0\)).

Publicly, there are three built-in scalar values that depend on the internal crustal thickness factor \(F(t)\):

  • Crustal thickness (in kms): \(T(t)\)

    The crustal thickness is calculated as:

    \(T(t) = F(t) \, T(t_{initial})\)

    By default, the initial crustal thickness \(T(t_{initial})\) is 40 kms. But you can specify a different value for each initial geometry point:

    # Specify one initial crustal thickness (in kms) per initial point.
initial_crustal_thicknesses_in_kms = [...]

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      initial_points,
      initial_time = 100,
      # dict with a single entry that maps the crustal thickness scalar type to initial values...
      initial_scalars = { pygplates.ScalarType.gpml_crustal_thickness : initial_crustal_thicknesses_in_kms })

    The crustal thicknesses can be queried at any reconstruction time using pygplates.ReconstructedGeometryTimeSpan.get_crustal_thicknesses():

    reconstructed_crustal_thicknesses_in_kms = reconstructed_geometry_time_span.get_crustal_thicknesses(
      reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_crustal_thicknesses_in_kms:
   ...

    Note

    This is the equivalent of:

    reconstructed_crustal_thicknesses_in_kms = reconstructed_geometry_time_span.get_scalar_values(
      reconstruction_time,
      pygplates.ScalarType.gpml_crustal_thickness)
...

  • Crustal stretching factor: \(\beta(t) = \frac{T(t_{initial})}{T(t)}\)

    By default, the initial crustal stretching factor \(\beta(t_{initial})\) is 1. And so the crustal stretching factor is calculated as:

    \(\beta(t) = \frac{1}{F(t)}\)

    But you can specify a different \(\beta(t_{initial})\) value for each initial geometry point:

    # Specify one initial crustal stretching factor per initial point.
initial_crustal_stretching_factors = [...]

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      initial_points,
      initial_time = 100,
      # dict with a single entry that maps the crustal stretching factor scalar type to initial values...
      initial_scalars = { pygplates.ScalarType.gpml_crustal_stretching_factor : initial_crustal_stretching_factors })

    …where each crustal stretching factor is then calculated as:

    \(\beta(t) = \frac{\beta(t_{initial})}{F(t)}\)

    The crustal stretching factors can be queried at any reconstruction time using pygplates.ReconstructedGeometryTimeSpan.get_crustal_stretching_factors():

    reconstructed_crustal_stretching_factors = reconstructed_geometry_time_span.get_crustal_stretching_factors(
      reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_crustal_stretching_factors:
   ...

    Note

    This is the equivalent of:

    reconstructed_crustal_stretching_factors = reconstructed_geometry_time_span.get_scalar_values(
      reconstruction_time,
      pygplates.ScalarType.gpml_crustal_stretching_factor)
...

  • Crustal thinning factor: \(\gamma(t) = 1 - \frac{T(t)}{T(t_{initial})}\)

    By default, the initial crustal thinning factor \(\gamma(t_{initial})\) is 0. And so the crustal thinning factor is calculated as:

    \(\gamma(t) = 1 - F(t)\)

    But you can specify a different \(\gamma(t_{initial})\) value for each initial geometry point:

    # Specify one initial crustal thinning factor per initial point.
initial_crustal_thinning_factors = [...]

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      initial_points,
      initial_time = 100,
      # dict with a single entry that maps the crustal thinning factor scalar type to initial values...
      initial_scalars = { pygplates.ScalarType.gpml_crustal_thinning_factor : initial_crustal_thinning_factors })

    …where each crustal thinning factor is then calculated as:

    \(\gamma(t) = 1 - (1 - \gamma(t_{initial})) \, F(t)\)

    The crustal thinning factors can be queried at any reconstruction time using pygplates.ReconstructedGeometryTimeSpan.get_crustal_thinning_factors():

    reconstructed_crustal_thinning_factors = reconstructed_geometry_time_span.get_crustal_thinning_factors(
      reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_crustal_thinning_factors:
   ...

    Note

    This is the equivalent of:

    reconstructed_crustal_thinning_factors = reconstructed_geometry_time_span.get_scalar_values(
      reconstruction_time,
      pygplates.ScalarType.gpml_crustal_thinning_factor)
...

See also

Scalar values, for more details on how scalar values are queried when the requested reconstruction time is inside or outside the time range of the snapshots.

Tectonic subsidence

Tectonic subsidence is one of the built-in scalar values that evolves over time due to deformation. By default, the initial tectonic subsidence (at the initial time) is zero for each geometry point. However you can optionally specify your own initial tectonic subsidence values (using the initial_scalars argument of pygplates.TopologicalModel.reconstruct_geometry()):

# Specify one initial tectonic subsidence value (in kms) per initial point.
initial_tectonic_subsidences_in_kms = [...]

reconstructed_geometry_time_span = topological_model.reconstruct_geometry(
      initial_points,
      initial_time = 100,
      # dict with a single entry that maps the tectonic subsidence scalar type to initial values...
      initial_scalars = { pygplates.ScalarType.gpml_tectonic_subsidence : initial_tectonic_subsidences_in_kms })

Note

The default (zero tectonic subsidence at the initial time) does not require the initial_scalars argument to be specified.

The tectonic subsidence of each reconstructed geometry point at any reconstruction time can then be queried using pygplates.ReconstructedGeometryTimeSpan.get_tectonic_subsidences():

reconstructed_tectonic_subsidences_in_kms = reconstructed_geometry_time_span.get_tectonic_subsidences(
      reconstruction_time)

# If none of the points are active at 'reconstruction_time' then this will be 'None'.
if reconstructed_tectonic_subsidences_in_kms:
   ...

Note

This is the equivalent of:

reconstructed_tectonic_subsidences_in_kms = reconstructed_geometry_time_span.get_scalar_values(
      reconstruction_time,
      pygplates.ScalarType.gpml_tectonic_subsidence)
...

See also

Scalar values, for more details on how scalar values are queried when the requested reconstruction time is inside or outside the time range of the snapshots.

Deformation

This section covers deformation in pyGPlates.

Topological network

To model deformation, a topological network must first be created. This consists of a boundary polygon (resolved by intersecting boundary line segments, similar to topological closed plate polygons), optional interior rigid blocks, individual deforming points, and a triangulation (with vertices from boundary, rigid blocks and deforming points).

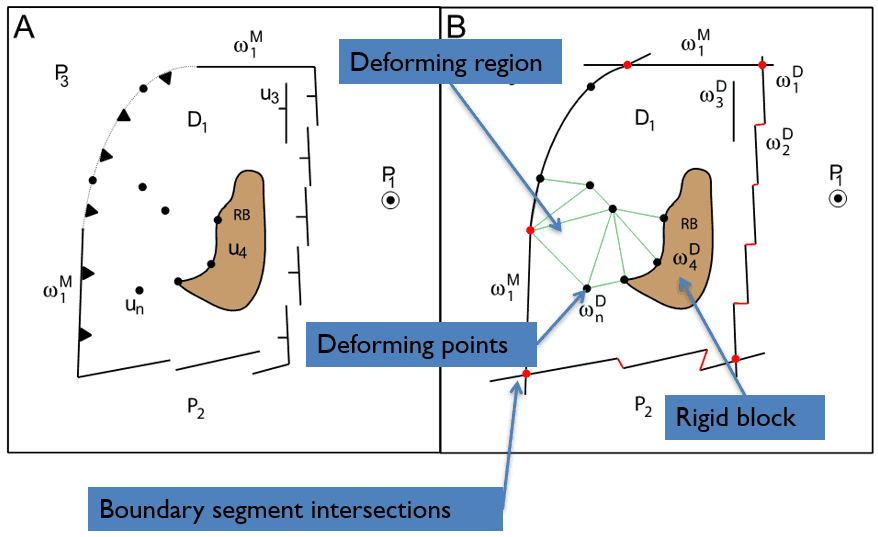
_images/DeformingNetworkDiagram.png

On the left are the elements that make up a topological network. On the right is the resolving of these elements at a reconstruction time to form a resolved topological network.

More information on topological networks in GPlates/pyGPlates can be found in the following paper:

Rigid blocks

A topological network can optionally have interior islands that are rigid.

Note

Any interior geometry of a network that is a polygon is considered a rigid block. And the interior rings (if any) of a rigid block polygon are ignored (ie, only the exterior ring applies).

Each rigid block is represented by a pygplates.ReconstructedFeatureGeometry, and is obtained from a pygplates.ResolvedTopologicalNetwork with:

rigid_blocks = resolved_topological_network.get_rigid_blocks()

For example, you can get the plate ID and boundary polygon of each interior rigid block (if any):

for rigid_block in rigid_blocks:
    rigid_block_plate_id = rigid_block.get_feature().get_reconstruction_plate_id()
    rigid_block_boundary = rigid_block.get_reconstructed_geometry()

Network triangulation

The network triangulation of a resolved topological network is the Delaunay triangulation of vertices obtained from the network’s boundary (polygon) and any interior rigid blocks (polygons) and any interior geometries (points or lines).

The Delaunay triangulation is a triangulation of the convex hull of its vertices. So it includes triangles outside the network boundary (and also includes triangles inside any interior rigid blocks). However, the deforming region of a network is defined to be inside the network’s boundary polygon (but outside its interior rigid block polygons, if any). Hence the triangulation contains triangles that are outside the deforming region. Therefore each triangle has a flag indicating whether it is inside the deforming region (if it’s centroid is in the deforming region) or not. These triangles in the deforming region of a network triangulation are referred to as the deforming triangulation.

Note

The Delaunay triangulation is not a constrained triangulation. This means the edges of some Delaunay triangles can cross over network boundary edges or interior block edges, rather than be constrained to follow them. However the flagging of Delaunay triangles (as deforming or non-deforming) deals with this quite effectively for current topological network datasets.

The deforming triangles in a network triangulation do not overlap any interior rigid blocks (other than the above-mentioned note about constrained triangulations). In other words, the deforming triangles (in the network triangulation) represent the deforming region of a resolved topological network and the rigid blocks (if any) represent the rigid regions.

A network triangulation is represented by a pygplates.NetworkTriangulation, and is obtained from a pygplates.ResolvedTopologicalNetwork with:

network_triangulation = resolved_topological_network.get_network_triangulation()

It consists of a sequence of vertices and a sequence of triangles. Each vertex is represented by a pygplates.NetworkTriangulation.Vertex and contains a position, a velocity, and a strain rate, and a list of incident vertices and incident triangles. Each triangle is represented by a pygplates.NetworkTriangulation.Triangle and contains a flag indicating whether it’s deforming or not, and contains a strain rate, and references three vertices and three adjacent triangles.

triangles = network_triangulation.get_triangles()
vertices = network_triangulation.get_vertices()

for triangle in triangles:
   triangle_is_in_deforming_region = triangle.is_in_deforming_region
   triangle_strain_rate = triangle.strain_rate

   for index in range(3):
      triangle_vertex = triangle.get_vertex(index)
      adjacent_triangle = triangle.get_adjacent_triangle(index)
      if adjacent_triangle:  # if not at a triangulation boundary
         ...

for vertex in vertices:
   vertex_position = vertex.position
   vertex_strain_rate = vertex.strain_rate
   vertex_velocity = vertex.get_velocity()  # a function optionally accepting various velocity calculation parameters

   for incident_vertex in vertex.get_incident_vertices():
      ...
   for incident_triangle in vertex.get_incident_triangles():
      ...

Strain rates in triangulation

Each triangle in a network triangulation is assigned a strain rate that is constant across the triangle (and is zero if the triangle is not deforming). Furthermore, the strain rate of each triangle can optionally be clamped to a maximum strain rate. Then each vertex in the triangulation is assigned a strain rate that is an area-weighted average of the (potentially clamped) strain rates from deforming triangles incident to the vertex.

Finally, the strain rate that is queried at an arbitrary location (within the deforming triangulation) is either assigned the strain rate of the triangle containing that location, or calculated by interpolating the strain rates of nearby vertices if strain rates are smoothed.

Note

Both strain rate clamping and smoothing affect strain rate queries (such as pygplates.ReconstructedGeometryTimeSpan.get_strain_rates()). They also affects strain queries (such as pygplates.ReconstructedGeometryTimeSpan.get_strains()), since strain is accumulated from strain rate.

Strain rate clamping

Strain rates can optionally be clamped to a maximum strain rate to avoid excessive or spurious extension/compression in some triangles of a deforming triangulation. This can happen in some topological networks depending on how they were built.

It is the total strain rate that is clamped, since it includes both the normal and shear components of deformation. When a strain rate is clamped, all components of its tensor (specifically its spatial gradients of velocity tensor) are scaled equally to ensure its total strain rate equals the maximum total strain rate.

Note

Clamping the total strain rate also limits quantities derived from strain rate such as crustal thinning and tectonic subsidence.

Strain rate clamping is determined by pygplates.ResolveTopologyParameters.enable_strain_rate_clamping when topological networks are resolved at a reconstruction time (using pygplates.TopologicalModel, pygplates.TopologicalSnapshot or pygplates.resolve_topologies()). And the maximum strain rate is pygplates.ResolveTopologyParameters.max_clamped_strain_rate. For example, to enable strain rate clamping (which is disabled by default) for a topological model, but keep the default maximum strain rate:

topological_model = pygplates.TopologicalModel(
   'topologies.gpml',
   'rotations.rot',
   default_resolve_topology_parameters = pygplates.ResolveTopologyParameters(
      enable_strain_rate_clamping = True))

Strain rate smoothing

Strain rates can optionally be smoothed to help reduce the faceted (piecewise constant) strain rate across a deforming triangulation (due to each triangle having a constant strain rate across its face).

Note

Smoothing the strain rate also affects quantities derived from strain rate such as crustal thinning and tectonic subsidence.

The strain rate at an arbitrary location within a deforming triangulation is affected by the smoothing value:

  • pygplates.StrainRateSmoothing.none - No smoothing. The strain rate is equal to the (constant) strain rate of the triangle containing the query location.

  • pygplates.StrainRateSmoothing.barycentric - Use linear interpolation of the strain rates of the 3 vertices of the triangle containing the query location.

  • pygplates.StrainRateSmoothing.natural_neighbour - Use natural neighbour interpolation of the strain rates of triangulation vertices near the query location.

Strain rate smoothing is determined by pygplates.ResolveTopologyParameters.strain_rate_smoothing when topological networks are resolved at a reconstruction time (using pygplates.TopologicalModel, pygplates.TopologicalSnapshot or pygplates.resolve_topologies()). For example, to disable strain rate smoothing (which is natural neighbour smoothing by default) for a topological model:

topological_model = pygplates.TopologicalModel(
   'topologies.gpml',
   'rotations.rot',
   default_resolve_topology_parameters = pygplates.ResolveTopologyParameters(
      strain_rate_smoothing = pygplates.StrainRateSmoothing.none))

Exponential rift stretching profile

A rift is typically modeled using two topological networks, one on each side of the rift axis. Each side of the rift axis typically has a single row of triangles (between the un-stretched side and the rift axis). As a result, the strain rate at any location within the rift will essentially be constant, even when the strain rates are smoothed. This is because triangulation vertices, along both the un-stretched boundary line and the rift axis, will effectively end up with the strain rate of the triangles (which is constant across each triangle).

To avoid the problem of constant stretching across the rift, an exponential rift stretching profile can be activated by adding rift left/right plate ID properties to a topological network feature.

Internally the exponential strain rate profile is implemented by automatically adding more points to the interior of a deforming triangulation and distributing the velocities at these points such that the strain rate varies exponentially (along the stretching direction) from the un-stretched side of the rift towards the rift axis.

Note

This works reasonably well for regular rifts (like AFR-SAM), but not as well for oblique rifts (like AUS-ANT).

Note

The exponential rift stretching profile affects quantities derived from strain rate such as crustal thinning and tectonic subsidence.

Rift left/right plate IDs

An exponential rift stretching profile is activated by adding a gpml:riftLeftPlate/gpml:riftRightPlate pair of conjugate plate ID properties to a topological network pygplates.Feature. This can be done, for example, by using the rift_parameters argument of pygplates.Feature.create_topological_network_feature(). The presence of these plate IDs triggers the internal generation of an exponential strain rate rift profile when the topological networks are resolved at a reconstruction time (using pygplates.TopologicalModel, pygplates.TopologicalSnapshot or pygplates.resolve_topologies()).

For example, to create a rift between Africa and South America:

SAM_rift_network = pygplates.GpmlTopologicalNetwork([...])
SAM_rift_feature = pygplates.Feature.create_topological_network_feature(
    SAM_rift_network,
    name='SAM rift',
    valid_time=(145, 115),
    rift_parameters=(201, 701))
SAM_rift_feature.set_reconstruction_plate_id(201)

AFR_rift_network = pygplates.GpmlTopologicalNetwork([...])
AFR_rift_feature = pygplates.Feature.create_topological_network_feature(
    AFR_rift_network,
    name='AFR rift',
    valid_time=(145, 115),
    rift_parameters=(201, 701))
AFR_rift_feature.set_reconstruction_plate_id(701)

Note

If the rift left/right plate ID properties are not present in a topological network feature then it is not considered a rift.

There are also three other parameters, in addition to the rift left/right plate IDs, that are optional and can either be set individually in each a topological network feature (eg, using the rift_parameters argument of pygplates.Feature.create_topological_network_feature()) or as default values for all topological network features (using pygplates.ResolveTopologyParameters).

Note

If these parameters are set in both places, then the feature properties have precedence.

When set on a topological network feature they become feature properties named:

  • gpml:riftExponentialStretchingConstant

  • gpml:riftStrainRateResolutionLog10 (note that this is \(\log_{10}\) of the rift strain rate resolution)

  • gpml:riftEdgeLengthThresholdDegrees

…and for features missing these properties these parameters are instead obtained from pygplates.ResolveTopologyParameters attributes:

…when the topological networks are resolved at a reconstruction time (using pygplates.TopologicalModel, pygplates.TopologicalSnapshot or pygplates.resolve_topologies()).

The default values (in pygplates.ResolveTopologyParameters()) should be fine for resolving rift features that do not contain the associated rift feature properties. But you can change the defaults as needed. For example, new default values can be specified for a topological model:

topological_model = pygplates.TopologicalModel(
   'topologies.gpml',
   'rotations.rot',
   default_resolve_topology_parameters = pygplates.ResolveTopologyParameters(
      rift_exponential_stretching_constant = 1.5,  # default is 1.0
      rift_strain_rate_resolution = 1e-16,         # default is 5e-17
      rift_edge_length_threshold_degrees = 0.2))   # default is 0.1

Rift exponential stretching constant

The strain rate in the rift stretching direction varies exponentially from the un-stretched side of the rift towards the rift axis. The spatial variation in strain rate is:

\[strain\_rate(x) = strain\_rate \times e^{C x} \frac{C}{e^C - 1}\]

…where \(strain\_rate\) is the un-subdivided, original (constant) strain rate, \(C\) is the rift exponential stretching constant and \(x = 0\) at the un-stretched side and \(x = 1\) at the stretched point. Therefore \(strain\_rate(0) < strain\_rate < strain\_rate(1)\). For example, when \(C = 1.0\) then \(strain\_rate(0) = 0.58 \times strain\_rate\) and \(strain\_rate(1) = 1.58 \times strain\_rate\).

Rift strain rate resolution

The rift strain rate resolution controls how accurately the actual strain rate curve (across rift profile) matches the exponential curve (in units of \(second^{-1}\)). Rift edges in the network triangulation are sub-divided until the strain rate matches the exponential curve (within this tolerance).

Rift edge length threshold

Rift edges in network triangulation shorter than the rift edge length threshold (in degrees) will not be further sub-divided.